Как сделать параллельный перенос фигуры

Теоретический урок по предмету математики для решения задач по теме "Параллельный перенос, поворот плоскости и подобные треугольники". Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка M отображается в такую точку M 1 , что два вектора равны. При параллельном переносе на вектор сохраняется расстояние между точками, то есть параллельный перенос — движение. Пусть x — коэффициент пропорциональности.

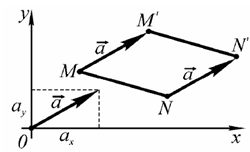
Тема 2. Параллельный перенос на координатной плоскости

Аналитическая геометрия для «чайников». Вернёмся к каноническому уравнению эллипса , а именно к условию , загадка которого уже давно терзает пытливые умы. Вот мы рассмотрели эллипс , но разве на практике не может встретиться уравнение? Ведь здесь , однако, это вроде бы как тоже эллипс! И да, это действительно эллипс, развеем мистику: В результате построения получен наш родной эллипс, повёрнутый на 90 градусов. То есть, — это неканоническая запись эллипса.

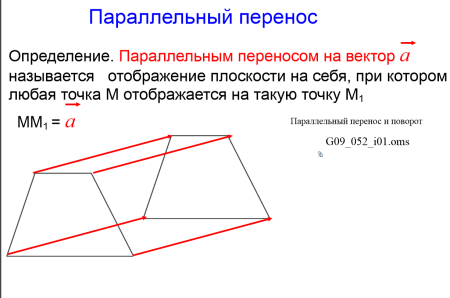
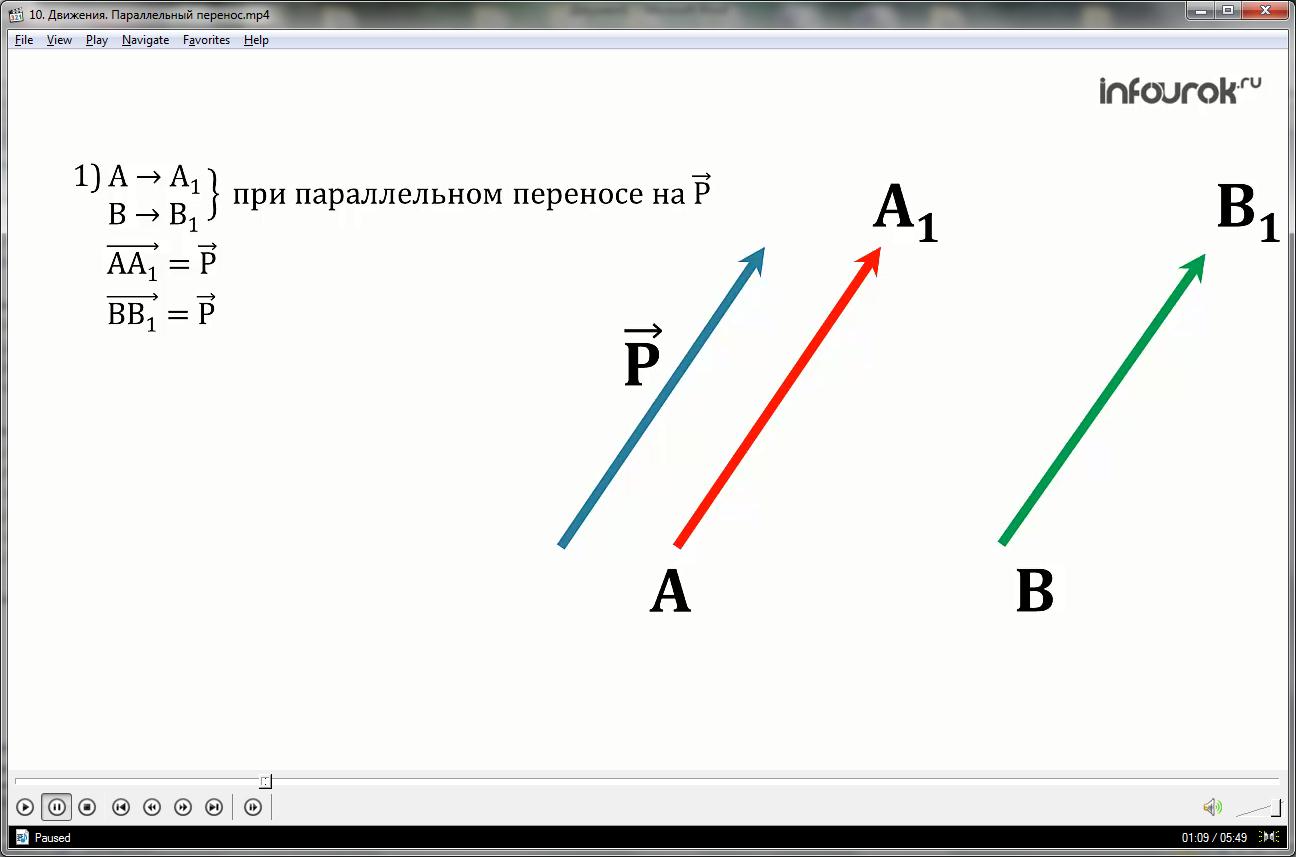
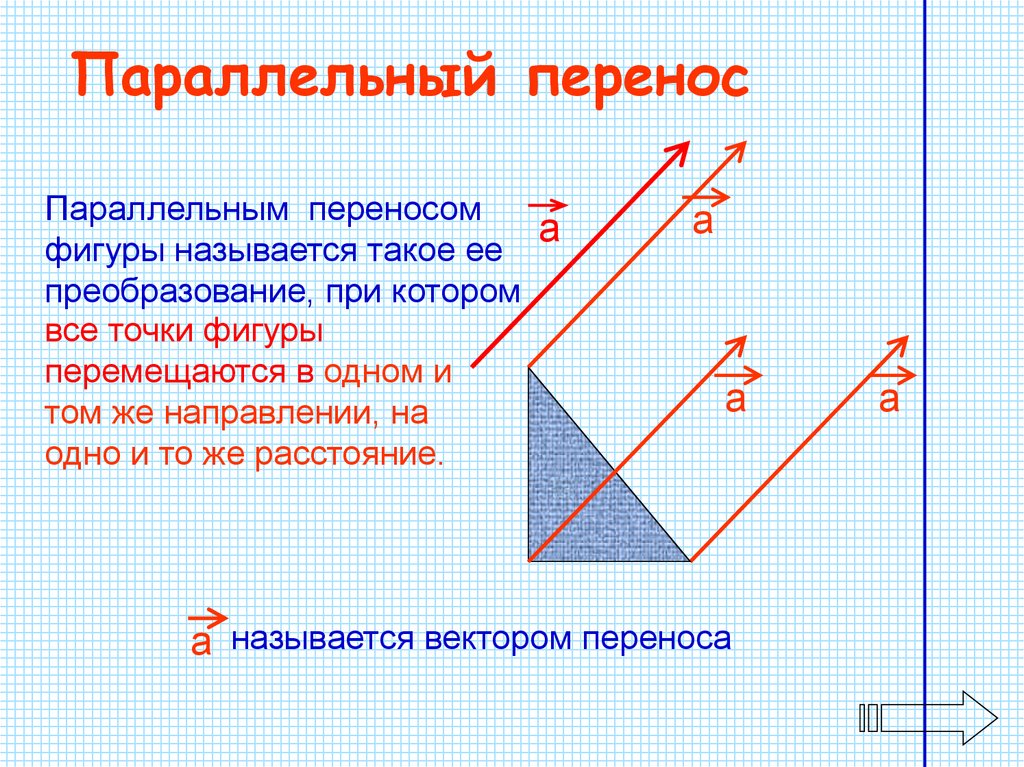
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние рис. Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение. Введем на плоскости декартовы координаты х, у. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.

Параллельный перенос представляет собой перемещение геометрической фигуры параллельно одной из плоскостей проекций. При этом величина проекции фигуры на эту плоскость не меняется. Еще одно важное свойство параллельного переноса заключается в том, что при любом перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. Если точка перемещается параллельно фронтальной плоскости, то её горизонтальная проекция движется по прямой, параллельной оси X. Определение натуральной величины плоской фигуры методами проецирования на дополнительную плоскость.

Похожие статьи

• Садовые фигурки из папье маше
• Поделка из шариков схемы - Схемы фигур из воздушных шаров Форум
• Дидактические игры своими руками в садик - Танграм своими руками (схемы игры, фигуры)
• Объемные фигуры из фанеры